Research (Theory)
SAC/SAC-CI in PCM: solvent effect in excited states
In PCM (polarizable continuum model), environmental effects such as solvent effects are modeled with polarizable continuum medium and the effects are calculated as apparent charges on the cavity that fits on the molecular structure of solute. We developed the SAC/SAC-CI in PCM method. [JCP 2010, JCP 2011] Combining environmental effects with nonvariational quantum chemical theories such as SAC/SAC-CI has not been well studied. Our method can consider the polarization of solvents that respond to the electronic transition of solute molecule. We can consider the polarization term that arises from the “electronic states of solvents”, which are neglected in usual classical approaches. The effect of “nonequilibrium solvation” can be treated by dividing the polarization into fast and slow components.
Using the SAC/SAC-CI in PCM, we can study solvatochromic shifts of absorption and emission spectra as fast processes, and optimizations of the excited state geometry in solution as slow processes.
The polarization of solvents that respond to the electronic transition of solute molecule is essentially important if the solute molecule has significantly different electron distributions or dipole moments between its ground and excited states. The results are also significantly different whether the solvent relaxation is treated as equilibrium or nonequilibrium.
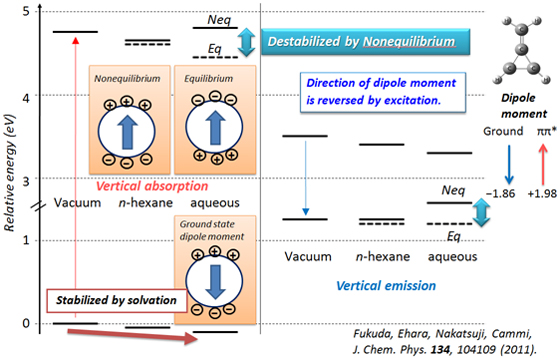
Relative energies of methylenecyclopropene (C4H4) in the ground and first excited states, where the ground state geometry was used for absorption and the excited states geometry was used for emission. Solid line denotes nonequilibrium solvation results and broken lines denote equilibrium solvation results.
CAP/SAC-CI method: resonance states
A “resonance” is an electronically metastable state, that is, a state of an (N+1)-electron system that lies energetically above the ground state of the associated N-electron system. and can consequently decay by electron autodetachment. We have developed the complex absorbing potential (CAP)/SAC-CI method to investigate the resonance states. The method has been implemented in the projected scheme and applied to the π* resonance state of formaldehyde. [CPL 2012]
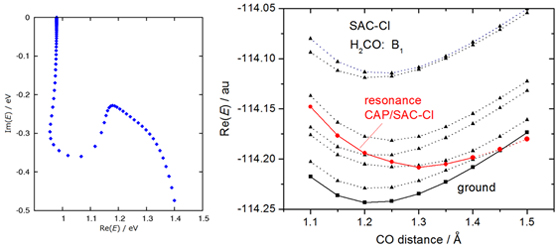
A typical η-trajectory obtained with the CAP/SAC-CI method is shown in left figure and the resonance state (resonance position and width) is identified. The right figure shows the potential energy curve of the resonance state embedded in the continuum along the C-O bond length.
SAC-CI general-R method (1998-)
Molecular excited states have complex electronic structure. For the theoretical study of the molecular excited states, it is relevant to describe these electronic states precisely. We are developing the highly accurate SAC-CI general-R theory [Nakatsuji, 1991] which can describe multi-electron processes and enabled reliable theoretical spectroscopy of the molecular excited states. We also implemented the analytical energy gradients of the general-R method. [CPL 1998, JCP 2004]

Active space SAC-CI method (2007-)
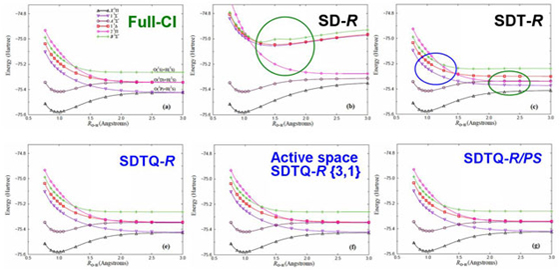
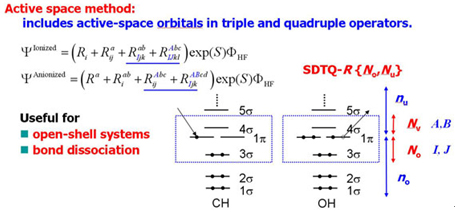
The SAC-CI general-R method is useful for the high accuracy calculations of the multi-electron processes. It is also applicable to the excited/ionized states of the open-shell systems. However, the computation of the general-R method is expensive. Piecuch et al. developed the active space method for the open-shell system which is accurate for the multi-electron processes with reasonable computational cost. Recently, we have developed the active space SAC-CI method. [JCP 2007, MP 2009, TCA 2012] In the active space method, higher operators like triple and quadruple operators includes excitation within active orbitals.
The active method was applied to the ground and excited states of the open-shell CH and OH radicals. Figure compares the potential energy curves of OH. The SD-R method is not sufficient for the higher excited states even at the equilibrium bond distance. The SDT-R method cannot describe the bond dissociation for some excited states. The SDTQ-R and its active space method reproduce the fine details of the potential energy curves.